Mrthfx

p • d • e Ogólna teoria względności Równanie Einsteina Testy doświadczalne Koncepcje podstawowe Geometria Riemanna Ogólna teoria względności Linia świata Szczególna teoria względności Zasada równoważności Gμν+Λgμν=8πGc4Tμν{displaystyle G_{mu nu }+Lambda g_{mu nu }={8pi G over c^{4}}T_{mu nu },} Zjawiska Czarna dziura Efekt geodezyjny Efekt Lense-Thirringa Fale grawitacyjne Horyzont zdarzeń Osobliwość grawitacyjna Problem Keplera Soczewkowanie grawitacyjne Równania Formalizm ADM Formalizm BSSN Grawitacja liniowa Grawitacyjna całka działania Parametryczny formalizm postnewtonowski Równania Friedmana Równanie Einsteina Teorie zaawansowane Grawitacja kwantowa Teoria Kaluzy-Kleina Metryki Friedmana-Lemaître'a-Robertsona-Walkera Gödla Kasnera Kerra Kerra-Newmana Reissnera–Nordströma Schwarzschilda Uczeni Subramanyan Chandrasekhar Arthur S. Eddington Albert Einstein Aleksandr Friedman Stephen Hawking Roy P. Kerr Georges Lemaître Josef Lense Hermann Minkowski Howard P. Robertson Karl Schwarzschild Hans Thirring

Kosmologia fizyczna

Wszechświat (chronologia • kształt • rozmiar • wiek) Wielki Wybuch Wczesny Wszechświat Inflacja • Nukleosynteza Promieniowania tła: grawitacyjne • mikrofalowe • neutrinowe Rozszerzający się Wszechświat ekspansja przestrzeni • metryka FLRW • poczerwienienie • prawo Hubble’a • równania Friedmana Powstawanie struktur wielka grupa kwazarów • kształt Wszechświata • powstawanie galaktyk • powstawanie struktur • rejonizacja • struktury wielkoskalowe Przyszłość Wszechświata śmierć cieplna Wszechświata • Wielki Kolaps • Wielkie Rozdarcie • Wszechświat Friedmana Składowe ciemna energia • ciemna materia • model Λ-CDM Eksperymenty 2dF • BOOMERanG • COBE • Illustris • Planck • SDSS • WiggleZ • WMAP Znani uczeni Aaronson • Alfvén • Alpher • Bharadwaj • de Sitter • Dicke • Ehlers • Einstein • Ellis • Friedman • Gamow • Guth • Hawking • Hubble • Lemaître • Mather • Penrose • Penzias • Rubin • Schmidt • Smoot • Suntzeff • Suniajew • Tolman • Wilson • Zeldowicz • i inni...

pokaż • dyskusja • edytuj

Symulacja przejścia czarnej dziury przed galaktyką (galaktyka w tle). Czarny punkt w środku to właśnie horyzont zdarzeń. Dookoła niego widać soczewkę grawitacyjną

Horyzont zdarzeń (ang. event horizon) − sfera otaczająca czarną dziurę lub tunel czasoprzestrzenny, oddzielająca obserwatora zdarzenia od zdarzeń, o których nie może on nigdy otrzymać żadnych informacji. Innymi słowy, jest to granica w czasoprzestrzeni, po przekroczeniu której prędkość ucieczki dla dowolnego obiektu i fali przekracza prędkość światła w próżni. I żaden obiekt, nawet światło emitowane z wnętrza horyzontu, nie jest w stanie opuścić tego obszaru. Wszystko, co przenika przez horyzont zdarzeń od strony obserwatora, znika.

Horyzont zdarzeń przypomina błonę półprzepuszczalną, gdyż z jednej strony nie przepuszcza fal elektromagnetycznych i innych sygnałów biegnących w kierunku obserwatora, natomiast przepuszcza je w kierunku przeciwnym. Obserwator, zmieniając swój ruch, sam może przeniknąć do części Wszechświata zakrytej przez horyzont zdarzeń.

Struktura pola grawitacyjnego (która wyznacza geometrię czasoprzestrzeni) oraz ruch obserwatora determinują istnienie horyzontu zdarzeń, jak i jego fizyczne znaczenie. W kontekście kosmologii, horyzont zdarzeń jest różny od horyzontu cząstek.

Do bardziej szczegółowych rodzajów horyzontów należą (powiązane ze sobą, choć odmienne) absolutny horyzont zdarzeń oraz horyzont pozorny, znajdujące się wokół czarnej dziury.

Inne pojęcia to: horyzont Cauchy’ego i martwy horyzont; orbity fotonowe i ergosfery Reissnera-Nordströma; horyzont cząstek i horyzonty kosmologiczne odnoszące się do kosmologii; a także izolowany horyzont i dynamiczny horyzont znaczące dla obecnego badania nad czarnymi dziurami.

Horyzont zdarzeń czarnej dziury |

Niekiedy określa się go jako granicę, w której prędkość ucieczki z czarnej dziury przewyższa prędkość światła w próżni. Według innego opisu, wszystkie trajektorie światła (potencjalne trajektorie, po których mogą poruszać się fotony), a więc wszystkie trajektorie w górnym stożku światła cząstek wewnątrz horyzontu, zostają zakrzywione tak, aby pozostały wewnątrz czarnej dziury. Kiedy cząstka znajdzie się po wewnętrznej stronie horyzontu, jej ruch w kierunku wnętrza dziury jest równie nieuchronny jak przemieszczanie się naprzód w czasie i może być wręcz uznawany za równoważny temuż, w zależności od przyjętego systemu współrzędnych czasoprzestrzennych.

Powierzchnia ograniczona promieniem Schwarzschilda zachowuje się jak horyzont zdarzeń w nieobracającym się ciele, które mieści się wewnątrz tegoż promienia (w obracającej się czarnej dziurze mechanizm jest nieco inny). Promień Schwarzschilda danego obiektu jest proporcjonalny do jego masy. Dla masy Słońca wynosi on około 3 km, a dla masy Ziemi w granicach 9 mm. Dla czarnej dziury utworzonej poprzez kolaps grawitacyjny (mającej masę przekraczającą granicę TOV) dolny limit wynosi mniej niż 10 km (granica TOV nie jest dokładnie znana).

Definicja “horyzontu zdarzeń” autorstwa Hawkinga i Ellisa^[1], Misnera, Thorne’a i Wheelera^[2], a także Walda^[3] różni się od powyższej. Ich definicja wyklucza przedstawione poniżej horyzonty kosmologiczne oraz cząstkowe (podobnie jak horyzont pozorny), jednak obecnie wszystkie one występują pod wspólną nazwą “horyzont zdarzeń” (Zobacz, np. Peacock^[4]). Aby ułatwić rozróżnienie, niektórzy autorzy odnoszą się do bardziej specyficznej cechy horyzontu jako do „horyzontu absolutnego”. W kontekście czarnych dziur, horyzont zdarzeń prawie zawsze odnosi się do horyzontu absolutnego, jako odmienny od horyzontu pozornego.

Według teorii Stephena Hawkinga opublikowanej w styczniu 2014 horyzont zdarzeń czarnej dziury nie istnieje w znanej nam dotychczas formie, a fizyka kwantowa umożliwia ucieczkę z czarnej dziury energii oraz informacji^[5][6]. Według niego czarna dziura jedynie tymczasowo przetrzymuje materię oraz energię i oddaje je później w zmienionej formie. Teoria ta oznacza zwrot w rozumieniu zjawisk zachodzących w czarnych dziurach, które dotychczas opierały się na istnieniu absolutnego horyzontu zdarzeń, zastąpionego przez Hawkinga pozornym. Jeśli teoria okaże się prawdziwa, to pozwoli wyjaśnić paradoks ściany ognia, który wynika z różnic postrzegania horyzontu zdarzeń zgodnie z zasadami fizyki klasycznej oraz zasadami fizyki kwantowej.

Horyzont zdarzeń dostrzegalnego Wszechświata |

Horyzont cząstek obserwowalnego Wszechświata jest to granica wyrażająca maksymalną odległość, dla jakiej zdarzenia mogą być obserwowane w chwili obecnej. Dla zdarzeń poza tą granicą światło nie miało czasu, by osiągnąć nasze położenie, nawet jeśli było emitowane w czasie powstania Wszechświata. Jak w czasie zmienia się horyzont cząstek zależy to od rozwoju Wszechświata. Z rozwiązania Aleksandra Friedmana dla równań Einsteina wynika, że kosmos (jego przyszłość i przeszłość) jest uzależniona od trzech parametrów – H określa tempo rozszerzania się Wszechświata, Omega jest miarą średniej gęstości materii we Wszechświecie i Lambda, czyli energia związana z pustą przestrzenią zwana inaczej „ciemną energią”. Dla horyzontu Wszechświata najważniejszy będzie współczynnik Omega (właściwie to Omega + Lambda). Jeśli Omega jest mniejsza niż 1 to Wszechświat nie posiada wystarczającej ilości materii żeby wyhamować swoją ekspansję, więc będzie on się rozszerzał aż umrze w Wielkim Chłodzie. Jeśli natomiast Omega jest większa niż 1, to Wszechświat posiada odpowiednią ilość materii, by wyhamować ekspansję, zawróci i zginie w Wielkim Kolapsie. Jeśli Omega wynosi 1, to horyzont Wszechświata będzie się rozszerzał, ale nie umrze, bo zależność masy od energii jest odpowiednia. Istnieją części Wszechświata, których nigdy nie da się zaobserwować, bez względu na to jak długo obserwator będzie czekał na dotarcie światła z tamtych regionów. Granica w przestrzeni, poza którą zdarzenia nie mogą być obserwowane, jest horyzontem zdarzeń, i oznacza maksymalny zasięg horyzontu cząstek.

Kryterium określania istnienia horyzontu cząstek dla Wszechświata przedstawia się następująco. Określ współporuszającą się odległość dE{displaystyle d_{E}} jako:

dE=∫t0∞ca(t)dt .{displaystyle d_{E}=int _{t_{0}}^{infty }{frac {c}{a(t)}}dt .}

W tym równaniu a jest czynnikiem skali, c jest prędkością światła w próżni, t₀ natomiast jest wiekiem Wszechświata. Jeśli dE→∞{displaystyle d_{E}rightarrow infty }, punkty dowolnie odległe mogą być obserwowane, i żaden horyzont zdarzeń nie istnieje. Jeśli dE≠∞{displaystyle d_{E}neq infty }, horyzont występuje.

Przykłady modeli kosmologicznych bez horyzontu zdarzeń są wszechświatami zdominowanymi przez materię lub przez promieniowanie. Przykładem modelu kosmologicznego z horyzontem zdarzeń jest kosmos zdominowany przez stałą kosmologiczną (wszechświat de Sittera).

Horyzont zdarzeń przyspieszającej cząstki |

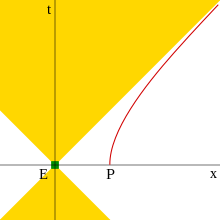
Diagram czasoprzestrzeni zawierający jednostajnie przyspieszoną cząstkę, P oraz zdarzenie E będące poza horyzontem zdarzeń tej cząstki. Przyszły stożek świetlny zjawiska nigdy nie przetnie się z linią świata cząstki.

Jeżeli dana cząstka porusza się ze stałą prędkością w nierozszerzającym się wszechświecie wolnym od pól grawitacyjnych, dowolne zdarzenie mające miejsce w tym wszechświecie będzie w końcu zaobserwowane przez tę cząstkę, ponieważ przyszły stożek świetlny pochodzący od tych zdarzeń przetnie się z linią świata cząstki. Jeżeli natomiast nasza cząstka porusza się z pewnym przyspieszeniem to w pewnych sytuacjach stożki świetlne niektórych zdarzeń zachodzących w tym wszechświecie nigdy nie przetną się z linią świata cząstki. Zgodnie z tymi założeniami horyzont zdarzeń reprezentuje w układzie odniesienia cząstki granicę, poza którą żadne zdarzenia nie będą nigdy zaobserwowane.

Przykładowo, zjawisko takie istnieje dla jednolicie przyspieszającej cząstki. Diagram czasoprzestrzeni opisujący taką sytuację przedstawiony jest po prawej stronie. W miarę jak cząstka przyspiesza, zbliża się, ale w swoim układzie odniesienia nigdy nie osiąga prędkości światła w próżni. Na diagramie czasoprzestrzeni jej trasą jest hiperbolą, której asymptota zbliża się do prostej o nachyleniu 45 stopni, będącej śladem promienia świetlnego ograniczającego stożek świetlny zdarzenia. Zdarzenie dla którego granicą stożka świetlnego jest ta właśnie asymptota, lub jest od niej oddalony, nie może być nigdy zaobserwowane przez przyspieszającą cząstkę. W układzie odniesienia cząstki istnieje granica spoza której nie dotrze żaden sygnał – horyzont zdarzeń.

Doświadczalnie możemy stworzyć zbliżone sytuacje (na przykład w akceleratorach cząstek), lecz prawdziwy horyzont zdarzeń nie zaistnieje – cząstka musiała by być przyspieszana w nieskończoność, co wymagałoby wyjątkowo dużych energii i urządzeń.

Oddziaływanie z horyzontem zdarzeń |

Błędna hipoteza dotycząca horyzontów zdarzeń, w szczególności horyzontów zdarzeń czarnej dziury, głosi, że stanowią one niezmienną powierzchnię niszczącą przedmioty zmierzające w jej kierunku. W rzeczywistości, wszystkie horyzonty zdarzeń wydają się znajdować w pewnej odległości od jakiegokolwiek obserwatora. Co więcej, obserwator wewnętrzny nie jest w stanie zarejestrować momentu przekroczenia tej granicy przez obiekty wysłane w jego kierunku (ponieważ stożek świetlny, który przekroczył już granicę horyzontu zdarzeń, nigdy nie przetnie orbity obserwatora zewnętrznego). Próba zbliżenia obiektu do nieruchomego horyzontu zdarzeń w stosunku do zewnętrznego obserwatora wymagałaby zastosowania siły nieograniczonej (stającej się nieskończoną) w miarę zbliżania się obiektu do jego granic.

W przypadku horyzontu postrzeganego przez obserwatora poruszającego się ruchem jednostajnie przyspieszonym w pustej przestrzeni, horyzont zdarzeń wydaje się pozostawać w stałej odległości od tegoż obserwatora, niezależnie od sposobu poruszania się obiektów w jego otoczeniu. Zmiana przyśpieszenia obserwatora może spowodować zmianę położenia horyzontu lub nawet uniemożliwić jego powstanie, w zależności od funkcji wybranego przyspieszenia. Obserwator ten nigdy nie będzie w stanie zbliżyć się do granicy horyzontu zdarzeń, ani przekroczyć miejsca, w którym powinno się pojawić.

W przypadku horyzontu postrzeganego przez obserwatora znajdującego się we Wszechświecie de Sittera, horyzont ten zawsze znajduje się w określonej odległości od obserwatora poruszającego się w inercjalnym układzie odniesienia. Obserwator ten nigdy nie będzie w stanie zbliżyć się do granic horyzontu zdarzeń, nawet jeśli przyspiesza.

W przypadku horyzontu otaczającego czarną dziurę, obserwatorzy nieruchomi w stosunku do odległego przedmiotu, będą mogli ustalić, gdzie znajduje się horyzont. Mimo że zbliżenie obserwatora do granicy horyzontu przy pomocy liny wydaje się być prawdopodobne, to w rzeczywistości jest to niemożliwe. Jeśli obserwator obniżany jest bardzo wolno, wówczas na układzie odniesienia obserwatora, horyzont wydaje się być bardzo daleko i z tego względu niezbędna jest dłuższa lina, żeby przekroczyć granicę horyzontu. Jeśli obserwator jest obniżany bardzo szybko przez innego obserwatora, wtedy rzeczywiście, pierwszy obserwator i część liny mogą dotknąć albo nawet skrzyżować się z horyzontem zdarzeń drugiego obserwatora. Jeśli lina jest bardzo mocno naciągnięta w celu wyłowienia pierwszego obserwatora z zasięgu horyzontu, wówczas siły wzdłuż liny rosną (stając się nieskończone), w miarę zbliżania się do granic horyzontu, wskutek czego lina musi pęknąć. Co więcej, pęknięcie to nie wystąpi w granicach horyzontu zdarzeń, ale w punkcie dostrzegalnym przez drugiego obserwatora.

Niemożliwym jest włożenie sztywnego pręta do horyzontu zdarzeń czarnej dziury. Jeśli przedmiot ten jest zbliżany bardzo powoli, wówczas prędkość jest zawsze za mała, żeby dotrzeć do horyzontu zdarzeń, ponieważ metalowa konstrukcja na końcu pręta ulega silnej kondensacji. Z punktu widzenia obserwatora znajdującego się na końcu tego pręta, horyzont zdarzeń jest niemożliwy do osiągnięcia. Jeśli pręt jest zbliżany bardzo szybko, pojawiają się te same problemy, co w przypadku wcześniej wspomnianej liny: pręt musi pęknąć, a odłamane części wpadają nieuchronnie do środka horyzontu zdarzeń.

Owe osobliwości mogą wystąpić jedynie wtedy, gdy przyjmiemy, że obserwatorzy zewnętrzni znajdują się w stałej odległości od obserwatora wewnętrznego. Obserwatorzy, którzy wpadną do środka czarnej dziury, poruszają się proporcjonalnie w stosunku do zewnętrznego obserwatora, dzięki czemu postrzegają sam horyzont, jak gdyby znajdował się w innym położeniu wobec wewnętrznego obserwatora. Jedynym widocznym skutkiem są zwiększające się siły pływowe (co może skutkować zapadnięciem się czarnej dziury w centralnym jej punkcie, zwanym osobliwością). Mimo że wydaje się to umożliwiać wewnętrznemu obserwatorowi otrzymywanie informacji od obiektów (znajdujących się na zewnątrz postrzeganego przez niego horyzontu, ale wewnątrz horyzontu widzianego przez zewnętrznego obserwatora), w rzeczywistości horyzont zdarzeń oddala się od zewnętrznego obserwatora do tego stopnia, że po pewnym czasie obserwator ten nie otrzymuje żadnego sygnału im dalej w głąb czarnej dziury. W wyniku czego, obaj obserwatorzy przekroczyli „coś”, co obserwator zewnętrzny odebrał jako horyzont zdarzeń, i ten proces percepcji (i jakiejkolwiek retransmisji) nie mógł być dostrzeżony przez obserwatora zewnętrznego.

Poza ogólną teorią względności |

Uważa się, że opis horyzontów zdarzeń przyjęty przez ogólną teorię względności nie jest kompletny. Kiedy warunki powstawania czarnych dziur modelowane są na podstawie bardziej całościowego obrazu (t.j. zarówno ogólnej teorii względności jak i mechaniki kwantowej), horyzonty zdarzeń mają trochę inne właściwości.

Obecnie przewiduje się, że podstawowym wpływem efektów kwantowych jest niezerowa temperatura horyzontu, a co za tym idzie – emitowanie promieniowania. Zjawisko czarnych dziur w ujęciu teorii promieniowania Hawkinga, podobnie jak i dalej idąca kwestia kreowania temperatury, jest częścią rozważań termodynamiki czarnej dziury. Zjawisko przyśpieszenia cząstek w ujęciu efektu Unruha-Daviesa powoduje, że przestrzeń wokół cząstki jest wypełniona materią i promieniowaniem.

Do pełnego opisu horyzontu zdarzeń wymagana jest przynajmniej teoria grawitacji kwantowej. Kandydatem na taką teorię jest M-teoria.

Zobacz też |

Zobacz hasło horyzont zdarzeń w Wikisłowniku

• horyzont akustyczny


• promieniowanie Hawkinga


• hipoteza kosmicznej cenzury

Przypisy |

Bibliografia |

• S.W. Hawking, G.F.R. Ellis: The large scale structure of space-time. Cambridge University Press, 1975.


• J.A. Peacock: Cosmological Physics. Cambridge University Press, 1999.


• K.S. Thorne, Charles Misner, John Wheeler: Gravitation. W. H. Freeman and Company, 1973.


• Robert M. Wald: General Relativity. University of Chicago Press, 1984.

• Zeeya Merali: Stephen Hawking: 'There are no black holes' (ang.). Nature, 2014-1-24. [dostęp 2014-02-01].


• S.W. Hawking: Information Preservation and Weather Forecasting for Black Holes. arxiv 1401.576, 2014. [dostęp 2014-02-10].

Literatura |

• M. Demiański: Astrofizyka relatywistyczna.


• B. Greene: Piękno Wszechświata. Prószyński i S-ka, 2006.


• S.W. Hawking: Wszechświat w skorupce orzecha.


• M. Kaku: Wszechświaty równoległe. Prószyński i S-ka, 2006.


• M. Kaku: Hiperprzestrzeń. Prószyński i S-ka, 2005.


• K.S. Thorne: Black Holes and Time Warps. W. W. Norton, 1994.