Mrthfx

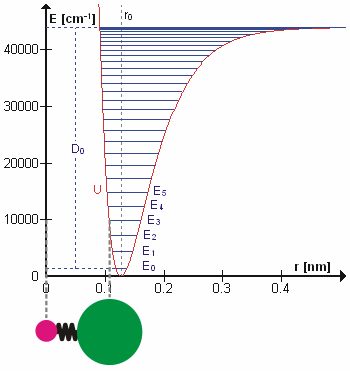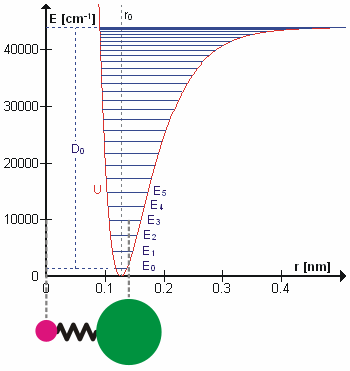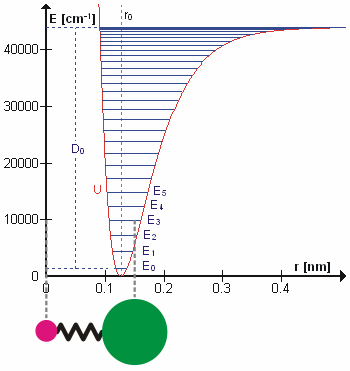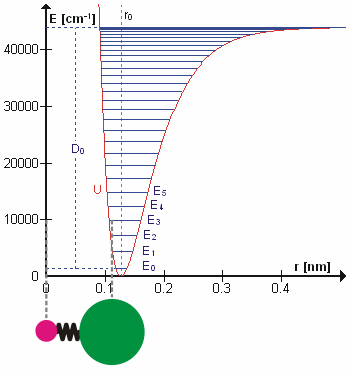
Cząsteczka HCl jako oscylator kwantowy drgający na poziomie energii E₃. Energia jest skwantowana, tzn. może przyjmować tylko skokowe wartości E₀, E₁... D₀ jest energią dysocjacji, r₀ średnią odległością atomów, U energią potencjalną ich ruchu oscylacyjnego. Atom wodoru umieszczono w początku układu współrzędnych, aby pokazać zmiany średniej odległości atomów na krzywej.

Kwantowy oscylator harmoniczny – układ fizyczny rozmiarów atomowych lub subatomowych (np. jon w sieci krystalicznej lub w cząsteczka gazu) wykonujący ruch drgający (oscylacyjny) pod wpływem siły proporcjonalnej do wychylenia od położenia równowagi. Właściwy opis ruchu wymaga zastosowania mechaniki kwantowej, co sprowadza się do znalezienia rozwiązań równania Schrödingera. Dowodem eksperymentalnym konieczności zastosowania mechaniki kwantowej do opisu właściwości mikroskopowych układów drgających jest np. nieciągłe widmo promieniowania emitowane przez drgające cząsteczki. Makroskopowym odpowiednikiem oscylatora kwantowego jest klasyczny oscylator harmoniczny, którym jest ciało makroskopowe o stosunkowo dużej masie, zawieszone np. na sprężynie i wykonujące drgania; do opisu jego ruchu wystarczająca jest mechanika klasyczna. Pojęcie oscylatora ma duże zastosowanie i znaczenie w wielu działach fizyki klasycznej i kwantowej.

Znaczenie oscylatora harmonicznego |

Teoria oscylatora harmonicznego ma w fizyce doniosłe znaczenie. Jest tak dlatego, że wiele różnych układów fizycznych jest opisywanych równaniami o postaci identycznej z postacią pojedynczego oscylatora lub zespołu oscylatorów harmonicznych, które są słabo ze sobą sprzężone (czyli słabo ze sobą oddziałują). W pierwszym przybliżeniu zaniedbuje się oddziaływanie – wtedy układ jest matematycznie równoważny prostemu do opisu układowi niezależnie drgających oscylatorów harmonicznych^[1], np. wszystkie cząstki wieloatomowe wykonują drgania, które z dobrym przybliżeniem można opisywać w ramach teorii oscylatorów harmonicznych.

Początki fizyki kwantowej wiążą się z pojęciem oscylatora kwantowego. Mianowicie Max Planck, próbując wyjaśnić zjawisko promieniowania termicznego ciał (tzw. zjawisko promieniowania ciała doskonale czarnego), przyjął, że cząstki materii emitujące i absorbujące promieniowanie zachowują się jak oscylatory. Planck założył, że energia oscylatora nie może być dowolna, lecz jest skwantowana, to znaczy może przyjmować tylko ściśle określone wartości. Założenie to nie posiadało wtedy żadnego uzasadnienia w znanych teoriach fizycznych.

Ważnym osiągnięciem było opisanie pola elektromagnetycznego jako pola kwantowego (tzw. drugie kwantowanie). W początkach rozwoju teorii kwantowej pole elektromagnetyczne traktowano jako pole klasyczne, będące źródłem potencjału A(r,t) oddziałującego na cząstki naładowane, wstawianym np. do równania Schrödingera (nierelatywistycznego), a nawet do relatywistycznego równania Diraca. Jednak dokładny opis pól kwantowych wymaga potraktowania ich jako układów kwantowych, gdzie równania pola są analogiczne do równań oscylatorów kwantowych^[1]. Ze względu na to, że pola kwantowe mają charakter bozonowy lub fermionowy, odpowiadające im oscylatory określa się jako oscylatory bozonowe i fermionowe (patrz niżej).

Klasyczny oscylator harmoniczny |

 Osobny artykuł: Klasyczny oscylator harmoniczny.

Klasyczny oscylator harmoniczny – to ciało o masie m,{displaystyle m,} na które działa siła proporcjonalna do wychylenia x{displaystyle x} ciała od stanu równowagi i mająca przeciwny zwrot

F=−kx,{displaystyle F=-kx,}

gdzie k{displaystyle k} jest stałą wielkością (tzw. stałą sprężystości). Przykładem oscylatora harmonicznego jest ciało na sprężynie, wykonujące niewielkie drgania od położenia równowagi, co zapewnia słuszność założenia o proporcjonalności siły do wychylenia (dla dużych wychyleń założenie to nie byłoby słuszne). Układ drgający ma energię potencjalną:

U(x)=12kx2=12mω2x2,{displaystyle U(x)={frac {1}{2}}kx^{2}={frac {1}{2}}momega ^{2}x^{2},}

która jest tym większa, im większe jest rozciągnięcie sprężyny (ω=k/m{displaystyle omega ={sqrt {k/m}}} jest częstotliwością kołową ruchu drgającego). Energia całkowita układu jest sumą energii kinetycznej i potencjalnej

E=p22m+U(x),{displaystyle E={frac {p^{2}}{2m}}+U(x),}

gdzie p=mv{displaystyle p=mv} oznacza pęd ciała drgającego w położeniu x.{displaystyle x.} Całkowita energia układu drgającego harmonicznie nie ulega zmianie w czasie, mimo że energia potencjalna zamienia się cyklicznie w energię kinetyczną i odwrotnie, kinetyczna przechodzi w potencjalną.

Kwantowy oscylator harmoniczny – przypadek stałej energii drgań |

Porównanie ruchu oscylatora harmonicznego klasycznego i kwantowego. (A–B) Oscylator klasyczny – to cząstka masywna (reprezentowana przez kulkę na sprężynie), której ruch można dobrze opisać za pomocą równań Newtona. (C–H) Oscylator kwantowy – to cząstka mikroskopowa, której ruch można poprawnie opisać jedynie za pomocą równania Schrödingera. Na rys. C–H pokazano niektóre w wielu możliwych funkcji falowych Ψ(x,t),{displaystyle Psi (x,t),} stanowiących rozwiązania równania Schrödingera. Na osi pionowej odłożono część rzeczywistą (kolor niebieski) oraz część urojoną (kolor czerwony) funkcji falowej, uzależnione od położenia cząstki x,{displaystyle x,} odłożonego na osi poziomej. Rys. C,D,E,F, ale nie G,H przedstawiają stany stacjonarne (o stałej energii). H przedstawia stan koherentny – stan kwantowy, który przybliża ruch oscylatora klasycznego.

W mechanice kwantowej do opisu ruchu układów fizycznych stosuje się zamiast równania Newtona równanie Schrödingera. Konkretna jego postać zależy od opisywanej sytuacji fizycznej. Jedną z metod znalezienia postaci równania Schrödingera w konkretnych przypadkach jest tzw. metoda kwantowania, polegająca na zamianie w równaniach ruchu mechaniki klasycznej pędu ciała p^{displaystyle {hat {p}}} na operator pędu. Współrzędne położenia ciała, np. x,{displaystyle x,} pozostawia się przy tym bez zmian (nadając mu teraz nazwę operatora położenia). (Słuszność tej metody uzasadnia fakt, że otrzymane za jej pomocą równania dają przewidywania zgodne z wynikami eksperymentów). W przypadku ruchu jednowymiarowego operator pędu ma postać:

p^=−iℏddx.{displaystyle {hat {p}}=-ihbar {frac {d}{dx}}.}

Ponieważ poszukiwany jest opis stanu układu w zależności od współrzędnych x,{displaystyle x,} dlatego trzeba znaleźć jawną postać równania Schrödingera w reprezentacji położeniowej, przy czym dla uproszczenia założymy, że energia układu jest niezmienna. (Podobnie zakłada się, rozwiązując zagadnienie poziomów energetycznych atomu wodoru). Jest to uzasadnione, jeżeli układ drgający pozostaje dłuższy czas w izolacji od otoczenia. Dlatego stosuje się równanie Schrödingera niezależne od czasu:

H^Ψ(x,t)=E Ψ(x,t).{displaystyle {hat {H}}Psi (x,t)=E Psi (x,t).}

gdzie E{displaystyle E} oznacza energię układu. Pozostaje znalezienie jawnej postaci operatora Hamiltona H^.{displaystyle {hat {H}}.} W tym celu do wyrażenia na energię całkowitą E{displaystyle E} oscylatora klasycznego (patrz wyżej) w miejsce klasycznego pędu p{displaystyle p} podstawia się operator pędu p^:{displaystyle {hat {p}}{:}}

H^=p^22m+12mω2x2.{displaystyle {hat {H}}={frac {{hat {p}}^{2}}{2m}}+{frac {1}{2}}momega ^{2}x^{2}.}

Podstawiając jawną postać operatora pędu, otrzymuje się ostatecznie:

H^=−ℏ22md2dx2+12mω2x2.{displaystyle {hat {H}}={frac {-hbar ^{2}}{2m}}{frac {d^{2}}{dx^{2}}}+{frac {1}{2}}momega ^{2}x^{2}.}

Równanie Schrödingera bez czasu przyjmuje więc postać:

−ℏ22md2dx2ψ(x)+12mω2x2ψ(x)=Eψ(x).{displaystyle {frac {-hbar ^{2}}{2m}}{frac {d^{2}}{dx^{2}}}psi (x)+{frac {1}{2}}momega ^{2}x^{2}psi (x)=Epsi (x).}

Rozwiązanie tego równania daje zbiór możliwych stanów stacjonarnych

ψn(x)=12nn!(mωπℏ)1/4⋅e−mωx22ℏ⋅Hn(mωℏx),n=0,1,2,…{displaystyle psi _{n}(x)={frac {1}{sqrt {2^{n},n!}}}left({frac {momega }{pi hbar }}right)^{1/4}cdot e^{-{frac {momega x^{2}}{2hbar }}}cdot H_{n}left({sqrt {frac {momega }{hbar }}}xright),quad n=0,1,2,dots }

Energia potencjalna oscylatora (niebieska parabola) i kilka pierwszych stanów własnych ψn(x){displaystyle psi _{n}(x)} w zależności od wielkości oscylacji x. Wykresy umieszczono na wysokościach odpowiadających energiom En{displaystyle E_{n}} tych stanów. Zaznaczono skok wartości energii ℏω.{displaystyle hbar omega .} Energia stanu podstawowego jest większa od zera. Widać też, że amplituda ruchu wzrasta z energią.

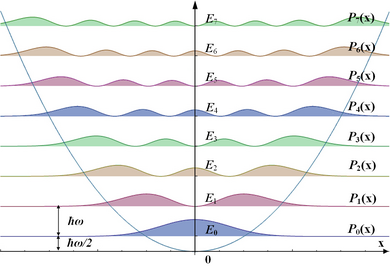
Gęstości prawdopodobieństwa Pn(x)=|ψn(x)|2{displaystyle P_{n}(x)=|psi _{n}(x)|^{2}} odpowiadające funkcjom falowym ψn(x).{displaystyle psi _{n}(x).} Z wykresów widać, że szansa znalezienia oscylatora w pobliżu maksymalnego wychylenia x od położenia równowagi jest największa. Odpowiada to sytuacji oscylatora klasycznego, który w punktach amplitudy przebywa najdłużej. U dołu – gęstość prawdopodobieństwa dla stanu podstawowego: widać, że w tym stanie oscylator najczęściej znajduje się w położeniu równowagi. Zaznaczono wartości energii En(x){displaystyle E_{n}(x)} odpowiadające rozkładom Pn(x).{displaystyle P_{n}(x).}

gdzie:

Hn(x)=(−1)nex2⋅dndxne−x2{displaystyle H_{n}(x)=(-1)^{n}e^{x^{2}}cdot {frac {d^{n}}{dx^{n}}}e^{-x^{2}}}

oznaczają wielomiany Hermite’a, gdzie np.

H0(x)=1,H1(x)=2x,H2(x)=(2x)2−2=4x2−2,H3(x)=(2x)3−6(2x)=8x3−12x,H4(x)=(2x)4−12(2x)2+12=16x4−48x2+12,…{displaystyle {begin{aligned}H_{0}(x)&=1,\H_{1}(x)&=2x,\H_{2}(x)&=(2x)^{2}-2=4x^{2}-2,\H_{3}(x)&=(2x)^{3}-6(2x)=8x^{3}-12x,\H_{4}(x)&=(2x)^{4}-12(2x)^{2}+12=16x^{4}-48x^{2}+12,\ldots end{aligned}}}

Postać funkcji falowych ψ0(x),…ψ7(x){displaystyle psi _{0}(x),dots psi _{7}(x)} pokazuje rysunek obok.

Stanom ψn(x){displaystyle psi _{n}(x)} odpowiadają energie oscylatora:

En=ℏω(n+12),n=0,1,2…{displaystyle E_{n}=hbar omega left(n+{frac {1}{2}}right),quad n=0,1,2ldots }

Układ kwantowy drgający harmonicznie przyjmuje tylko wyróżnione wartości energii, czym różni się od układu klasycznego (makroskopowego) – ten ostatni może drgać, mając dowolną wartość energii. Ponieważ drgające układy mikroskopowe faktycznie przyjmują dyskretne poziomy energii, widoczne się staje, że teoria Schrödingera dostarcza właściwego ich opisu.

Różnica między kolejnymi poziomami energii jest stała i wynosi ℏω.{displaystyle hbar omega .} Animacja u góry pokazuje, że poziomy rzeczywistej cząsteczki HCl dla większych energii En stopniowo zagęszczają się. Dla większych energii wzrasta amplituda i drgania przestają być harmoniczne, co było zakładane wcześniej. Opis takiego ruchu wymagałby dodania do Hamiltonianu dodatkowego wyrazu, odpowiadającego za nieharmoniczny składnik siły. Drugie spostrzeżenie: najmniejsza energia drgań nie jest zerowa, gdyż E0=1/2ℏω.{displaystyle E_{0}=1/2hbar omega .} Jest to tzw. energia drgań zerowych, która nie jest znana fizyce klasycznej. Istnienie tej energii oznacza, że układ kwantowy nigdy nie może być w absolutnym spoczynku.

Bozonowy oscylator harmoniczny |

Rozwiązanie równania Schrödingera oscylatora metodą bezpośrednią jest bardzo złożone. Powyżej został podany jedynie wynik. Jednak można uprościć poszukiwanie rozwiązania, stosując tzw. metodę algebraiczną^[2][3]. Metoda ta polega na zastąpieniu operatorów x,p^{displaystyle x,{hat {p}}} operatorami anihilacji a oraz kreacji a†.{displaystyle a^{dagger }.}

Operatory kreacji i anihilacji |

Operatory anihilacji i kreacji definiuje się następująco:

a=12(mωℏx+i1mωℏp^),{displaystyle a={frac {1}{sqrt {2}}}{bigg (}{sqrt {frac {momega }{hbar }}}x+i{frac {1}{sqrt {momega hbar }}}{hat {p}}{bigg )},}

a†=12(mωℏx−i1mωℏp^).{displaystyle a^{dagger }={frac {1}{sqrt {2}}}{bigg (}{sqrt {frac {momega }{hbar }}}x-i{frac {1}{sqrt {momega hbar }}}{hat {p}}{bigg )}.}

Operatory położenia x{displaystyle x} i pędu p^{displaystyle {hat {p}}} wyrażone przez te operatory mają postać:

x=ℏ2mω(a+a†),{displaystyle x={sqrt {frac {hbar }{2momega }}}(a+a^{dagger }),}

p^=imωℏ2(a†−a).{displaystyle {hat {p}}=i{sqrt {frac {momega hbar }{2}}}(a^{dagger }-a).}

Użyteczność metody algebraicznej bierze się stąd, że operatory a{displaystyle a} oraz a†{displaystyle a^{dagger }} dają proste reguły komutacjne, przy czym przez komutator rozumiane jest wyrażenie [A,B]=AB−BA{displaystyle [A,B]=AB-BA}

[a,a†]=1,{displaystyle [a,a^{dagger }]=1,}

[N,a]=−a,{displaystyle [N,a]=-a,}

[N,a†]=a†,{displaystyle [N,a^{dagger }]=a^{dagger },}

gdzie N=a†a{displaystyle N=a^{dagger }a} to tzw. operator liczby cząstek. Dzięki temu złożone przekształcenia zostają zastąpione prostszymi manipulacjami na symbolach.

Operator Hamiltona wyrażony przez te operatory przyjmuje postać:

H^=12ℏω(a†a+aa†)=ℏω(a†a+12),{displaystyle {hat {H}}={frac {1}{2}}hbar omega (a^{dagger }a+aa^{dagger })=hbar omega left(a^{dagger }a+{frac {1}{2}}right),}

przy czym ostatni wzór uzyskuje się, wykorzystując własność [a,a†]=1.{displaystyle [a,a^{dagger }]=1.} Niech |n⟩≡ψn{displaystyle |nrangle equiv psi _{n}} (w zapisie Diraca) oznacza stan własny oscylatora o energii En.{displaystyle E_{n}.} Ponieważ szukane są stany stacjonarne oscylatora, to należy rozwiązać równanie Schrödingera bez czasu:

H^|n⟩=ℏω(a†a+12)|n⟩=En|n⟩.{displaystyle {hat {H}}|nrangle =hbar omega left(a^{dagger }a+{frac {1}{2}}right)|nrangle =E_{n}|nrangle .}

Aby to zrobić, zostanie najpierw pokazane, jak operatory kreacji i anihilacji działają na stany oscylatora.

Działanie operatorów kreacji i anihilacji na stany własne oscylatora |

Mnożąc powyższe równanie z lewej strony przez a†,{displaystyle a^{dagger },} otrzymuje się

ℏω(a†a†a+12a†)|n⟩=Ena†|n⟩.{displaystyle hbar omega {bigg (}a^{dagger }a^{dagger }a+{frac {1}{2}}a^{dagger }{bigg )}|nrangle =E_{n}a^{dagger }|nrangle .}

Korzystając z komutatora [a,a†]=1,{displaystyle [a,a^{dagger }]=1,} dostaniemy:

ℏω((a†aa†a−a†)+12a†)|n⟩=Ena†|n⟩{displaystyle hbar omega {bigg (}(a^{dagger }aa^{dagger }a-a^{dagger })+{frac {1}{2}}a^{dagger }{bigg )}|nrangle =E_{n}a^{dagger }|nrangle }

i stąd

ℏω(a†a+12)(a†|n⟩)=(En+ℏω)(a†|n⟩),{displaystyle hbar omega left(a^{dagger }a+{frac {1}{2}}right)(a^{dagger }|nrangle )=(E_{n}+hbar omega )(a^{dagger }|nrangle ),}

czyli

H^(a†|n⟩)=(En+ℏω)(a†|n⟩).{displaystyle {hat {H}},(a^{dagger }|nrangle )=(E_{n}+hbar omega )(a^{dagger }|nrangle ).}

Wynika stąd, że stany (a†|n⟩){displaystyle (a^{dagger }|nrangle )} są stanami własnymi operatora Hamiltona, którym odpowiadają wartości własne (En+ℏω).{displaystyle (E_{n}+hbar omega ).} Inaczej patrząc na ten wynik, można powiedzieć, że operator a†,{displaystyle a^{dagger },} działając na dowolny stan |n⟩,{displaystyle |nrangle ,} tworzy stan o energii powiększonej o kwant ℏω{displaystyle hbar omega } względem energii En{displaystyle E_{n}} stanu, na który działa. Stąd nazwa tego operatora – operator kreacji.

Podobnie, mnożąc równanie Schrödingera przez operator anihilacji a{displaystyle a}

H^(a|n⟩)=(En−ℏω)(a|n⟩),{displaystyle {hat {H}},(a|nrangle )=(E_{n}-hbar omega )(a|nrangle ),}

co oznacza, że operator a, działając na dowolny stan |n⟩,{displaystyle |nrangle ,} tworzy stan o energii mniejszej o ℏω{displaystyle hbar omega } od energii En{displaystyle E_{n}} stanu, na który działa; stanowi a|n⟩{displaystyle a|nrangle } odpowiada bowiem energia (En−ℏω).{displaystyle (E_{n}-hbar omega ).}

Dokładne obliczenia pokazują, że działanie operatorów kreacji i anihilacji na stany własne jest następujące:

a|n⟩=n|n−1⟩,a†|n⟩=n+1|n+1⟩.{displaystyle {begin{aligned}aleft|nrightrangle &={sqrt {n}},left|n-1rightrangle ,\a^{dagger }left|nrightrangle &={sqrt {n+1}},left|n+1rightrangle .end{aligned}}}

Stan zerowy oscylatora i energie własne |

Aby znaleźć najniższy możliwy stan oscylatora zauważmy, że operator anihilacji, działając wielokrotnie na dany stan wyjściowy, będzie tworzył stany o coraz mniejszej energii. Ponieważ energia oscylacji nie może być mniejsza od zera, więc trzeba przyjąć, że istnieje stan najniższy, |0⟩,{displaystyle |0rangle ,} taki że działanie operatorem anihilacji na ten stan daje zero:

a|0⟩=0,{displaystyle a|0rangle =0,}

przy czym jeżeli w obliczeniach stan |0⟩{displaystyle |0rangle } zostanie wyzerowany, to działając następnie jakimkolwiek operatorem, otrzyma się nadal zero, czyli:

H^(a|0⟩)=(E0−ℏω)(a|0⟩)=0.{displaystyle {hat {H}},(a|0rangle )=(E_{0}-hbar omega )(a|0rangle )=0.}

Działając operatorem Hamiltona na stan zerowy, otrzyma się:

H^|0⟩=ℏω(a†a+12)|0⟩=12ℏωa†a|0⟩+12ℏω|0⟩=…=12ℏω|0⟩,{displaystyle {hat {H}}|0rangle =hbar omega {bigg (}a^{dagger }a+{frac {1}{2}}{bigg )}|0rangle ={frac {1}{2}}hbar omega a^{dagger }a|0rangle +{frac {1}{2}}hbar omega |0rangle =ldots ={frac {1}{2}}hbar omega |0rangle ,}

co oznacza, że energia stanu zerowego wynosi E0=12ℏω.{displaystyle E_{0}={frac {1}{2}}hbar omega .}

Ponieważ En+1=En+ℏω,{displaystyle E_{n+1}=E_{n}+hbar omega ,} to otrzymuje się wartości dowolnych energii własnych:

En=ℏω(n+12),n=0,1,…{displaystyle E_{n}=hbar omega {bigg (}n+{frac {1}{2}}{bigg )},quad n=0,1,dots }

Z powyższego wzoru widać, że oscylator bozonowy może przyjmować dowolną energię. Ilość kwantów energii w danym stanie bozonowym nie jest więc niczym ograniczona.

Wyrażenie stanów własnych za pomocą operatora kreacji |

Stany własne |n⟩{displaystyle |nrangle } można wyrazić za pomocą operatora kreacji a†{displaystyle a^{dagger }}

|n⟩=1n!(a†)n|0⟩.{displaystyle |nrangle ={frac {1}{sqrt {n!}}}(a^{dagger })^{n}|0rangle .}

Dowód:

⟨n|aa†|n⟩=⟨n|([a,a†]+a†a)|n⟩=⟨n|(N+1)|n⟩=n+1⇒a†|n⟩=n+1|n+1⟩⇒|n⟩=a†n|n−1⟩=(a†)2n(n−1)|n−2⟩=⋯=(a†)nn!|0⟩.{displaystyle {begin{aligned}langle n|aa^{dagger }|nrangle &=langle n|left([a,a^{dagger }]+a^{dagger }aright)|nrangle =langle n|left(N+1right)|nrangle =n+1\Rightarrow a^{dagger }|nrangle &={sqrt {n+1}}|n+1rangle \Rightarrow |nrangle &={frac {a^{dagger }}{sqrt {n}}}|n-1rangle ={frac {left(a^{dagger }right)^{2}}{sqrt {n(n-1)}}}|n-2rangle =cdots ={frac {left(a^{dagger }right)^{n}}{sqrt {n!}}}|0rangle .end{aligned}}}

Funkcja własna stanu zerowego |

Postać stanu próżni ma fundamentalne znaczenie, gdyż dopiero znając ten stan można dokonać obliczeń innych stanów.

Postać stanu |0⟩{displaystyle |0rangle } w reprezentacji położeniowej wyznacza się przedstawiając operator anihilacji w jawnej postaci, tj. podstawiając p^=−iℏddx{displaystyle {hat {p}}=-ihbar {frac {d}{dx}}} do wyrażenia na ten operator:

a=12(mωℏx+ℏmωddx).{displaystyle a={frac {1}{sqrt {2}}}left({sqrt {frac {momega }{hbar }}}x+{sqrt {frac {hbar }{momega }}}{frac {d}{dx}}right).}

Podstawiając stałą pomocniczą ξ=ℏmω,{displaystyle xi ={sqrt {frac {hbar }{momega }}},} operator anihilacji przyjmie postać

a=12(1ξx+ξddx).{displaystyle a={frac {1}{sqrt {2}}}left({frac {1}{xi }}x+xi {frac {d}{dx}}right).}

Stan |0⟩{displaystyle |0rangle } wyrażony w bazie położeniowej jest pewną funkcją zmiennej x,{displaystyle x,} tj. pewną funkcją ψ0(x)≡⟨x|0⟩,{displaystyle psi _{0}(x)equiv langle x|0rangle ,} ponieważ operator anihilacji działając na stan |0⟩{displaystyle |0rangle } ma go zerować, to musi być spełnione równanie

a[ψ0(x)]=0,{displaystyle a[psi _{0}(x)]=0,}

czyli

12(1ξx+ξddx)ψ0(x)=0.{displaystyle {frac {1}{sqrt {2}}}left({frac {1}{xi }}x+xi {frac {d}{dx}}right)psi _{0}(x)=0.}

Jest to równanie różniczkowe 1-go stopnia. Po znalezieniu rozwiązania i podstawieniu z powrotem wyrażenie na ξ,{displaystyle xi ,} otrzymuje się:

ψ0(x)=C0exp⁡(−mωℏx22),{displaystyle psi _{0}(x)=C_{0}exp left(-{frac {momega }{hbar }}{frac {x^{2}}{2}}right),}

gdzie C0{displaystyle C_{0}} – stała normalizacyjna. Funkcja ta jest funkcją wykładniczą, symetrycznie zanikającą w nieskończonościach, mającą maksimum dla x=0.{displaystyle x=0.} Oznacza to, że dla energii drgań zerowych największe jest prawdopodobieństwo znalezienia oscylatora w stanie równowagi (porównaj wykresy gęstości prawdopodobieństw |ψn(x)|2{displaystyle |psi _{n}(x)|^{2}} umieszczone w poprzednim rozdziale).

Funkcje własne stanów wzbudzonych |

Za pomocą operatora kreacji a†{displaystyle a^{dagger }} można teraz obliczyć funkcje falowe stanów wzbudzonych:

ψ1=a†ψ0,{displaystyle psi _{1}=a^{dagger }psi _{0},}

ψ2=12a†ψ1=12(a†)2ψ0,{displaystyle psi _{2}={frac {1}{sqrt {2}}}a^{dagger }psi _{1}={frac {1}{sqrt {2}}}(a^{dagger })^{2}psi _{0},}

ψn(x)=1n!(a†)nψ0.{displaystyle psi _{n}(x)={frac {1}{sqrt {n!}}}(a^{dagger })^{n}psi _{0}.}

Do obliczenia stanów wzbudzonych wystarczy znaleźć wynik działania potęgi operatora kreacji na stan zerowy. Operator a†{displaystyle a^{dagger }} w jawnej postaci uzyskuje się analogicznie jak w przypadku operatora a:{displaystyle a{:}}

a†=12(1ξx−ξddx).{displaystyle a^{dagger }={frac {1}{sqrt {2}}}left({frac {1}{xi }}x-xi {frac {d}{dx}}right).}

Powyższy operator różniczkowy, działając n-krotnie na funkcję wykładniczą ψ0=C0exp⁡(−mωℏx22),{displaystyle psi _{0}=C_{0}exp left(-{frac {momega }{hbar }}{frac {x^{2}}{2}}right),} reprodukuje ten sam czynnik wykładniczy, pomnożony przez wielomian n{displaystyle n}-tego rzędu względem x.{displaystyle x.}

Ostatecznie otrzymamy:

ψn(x)=1n!(a†)nψ0(x)=CnHn(xξ)ψ0(x),{displaystyle psi _{n}(x)={frac {1}{sqrt {n!}}}(a^{dagger })^{n}psi _{0}(x)=C_{n}H_{n}left({frac {x}{xi }}right)psi _{0}(x),}

gdzie:

Hn(x)=(−1)nex2dndxne−x2{displaystyle H_{n}(x)=(-1)^{n}e^{x^{2}}{frac {d^{n}}{dx^{n}}}e^{-x^{2}}}

są wielomianami Hermite’a, Cn{displaystyle C_{n}} jest stałą normalizacyjną, ξ=ℏmω.{displaystyle xi ={sqrt {frac {hbar }{momega }}}.}

Algebra Heisenberga |

Powyżej zdefiniowane operatory tworzą grupę operatorów

Xi={I,a,a†,N}.{displaystyle X_{i}=left{I,a,a^{dagger },Nright}.}

Grupa ta rozpina algebrę Heisenberga (która jest jedną z algebr Liego) o następujących komutatorach

[a,a†]=1,{displaystyle [a,a^{dagger }]=1,}

[a,a]=[a†,a†]=0,{displaystyle [a,a]=[a^{dagger },a^{dagger }]=0,}

[N,a]=−a,{displaystyle [N,a]=-a,}

[N,a†]=a†,{displaystyle [N,a^{dagger }]=a^{dagger },}

[I,Xi]=0.{displaystyle [I,X_{i}]=0.}

Fermionowy oscylator harmoniczny |

(1) Przypomnijmy, że bozonowy oscylator harmoniczny opisuje hamiltonian:

H^=12ℏω(a†a+aa†).{displaystyle {hat {H}}={frac {1}{2}}hbar omega (a^{dagger }a+aa^{dagger }).}

(2) Analogicznie definiuje się fermionowy oscylator harmoniczny – opisuje go hamiltonian:

H=12ℏω(c†c−cc†),{displaystyle H={frac {1}{2}}hbar omega (c^{dagger }c-cc^{dagger }),}

przy czym spełnione są związki:

{c,c†}=1,{displaystyle {c,c^{dagger }}=1,}

{c,c}={c†,c†}=0,{displaystyle {c,c}={c^{dagger },c^{dagger }}=0,}

gdzie:

c,c†{displaystyle c,c^{dagger }} – operatory anihilacji i kreacji pojedynczego fermionu (o częstotliwości ω{displaystyle omega }),

{..,..}{displaystyle {..,..}} – antykomutator operatorów, tj.

{c,c†}=cc†+c†c,{displaystyle {c,c^{dagger }}=cc^{dagger }+c^{dagger }c,}

{c,c}=cc+cc.{displaystyle {c,c}=cc+cc.}

Operator liczby fermionów ma postać

N=c†c.{displaystyle N=c^{dagger }c.}

Powyżej zdefiniowane operatory tworzą grupę operatorów

Xi={I,c,c†,N=c†c}.{displaystyle X_{i}={I,c,c^{dagger },N=c^{dagger }c}.}

Grupa ta rozpina algebrę gradowaną o następujących komutatorach

[N,c]=−c,{displaystyle [N,c]=-c,}

[N,c†]=c†,{displaystyle [N,c^{dagger }]=c^{dagger },}

[I,Xi]=0.{displaystyle [I,X_{i}]=0.}

(3) Hamiltonian fermionowy można przekształcić do postaci:

H=ℏω(c†c−12)=ℏωc†c+E0,{displaystyle H=hbar omega (c^{dagger }c-{frac {1}{2}})=hbar omega c^{dagger }c+E_{0},}

gdzie E0=−12ℏω{displaystyle E_{0}=-{frac {1}{2}}hbar omega } jest energią stanu podstawowego.

(4) Zakaz Pauliego

Reguła komutacyjna {c†,c†}=0{displaystyle {c^{dagger },c^{dagger }}=0} wyraża zakaz Pauliego:

• fermionowy oscylator harmoniczny istnieje tylko w stanie próżni |0⟩{displaystyle |0rangle } lub w pierwszym stanie wzbudzonym |1⟩=c†|0⟩,{displaystyle |1rangle =c^{dagger }|0rangle ,}
  


• drugi stan wzbudzony |2⟩=(c†)2|0⟩{displaystyle |2rangle =(c^{dagger })^{2}|0rangle } nie istnieje, bo z reguł antykomutacyjnych wynika, iż (c†)2=0{displaystyle (c^{dagger })^{2}=0} (czyli |2⟩=(c†)2|0⟩=0{displaystyle |2rangle =(c^{dagger })^{2}|0rangle =0}).

Operator Hamiltona – to operator energii. Dozwolonym stanom oscylatora odpowiadają wartości własne operatora Hamiltona:

• 
  E0=−12ℏω{displaystyle E_{0}=-{frac {1}{2}}hbar omega } – dla stanu |0⟩,{displaystyle |0rangle ,}
  


• 
  E1=+12ℏω{displaystyle E_{1}=+{frac {1}{2}}hbar omega } – dla stanu |1⟩.{displaystyle |1rangle .}
  

Kwantowa teoria pola |

Dokładnego opisu pól fizycznych dostarcza kwantowa teoria pola. Kwantowanie pól fizycznych polega na zastąpieniu wielkości polowych (skalarnych czy wektorowych) operatorami. Przy tym pola dzieli się na bozonowe (o spinie całkowitym) i fermionowe (o spinie połówkowym). Pola opisywane są za pomocą hamiltonianów analogicznych do hamiltonianu oscylatora harmonicznego bozonowego lub fermionowego.

Stan pola bozonowego (np. przypisanego fotonom, mające spin 1) opisuje się jako sumę wzbudzeń wielu oscylatorów bozonowych, z których każdy ma inną częstotliwość drgań i właściwą sobie energię (przy czym energie te są skwantowane, tj. mogą przyjmować dyskretne wartości En(ω)=ℏω(n+12),n=0,1,…,{displaystyle E_{n}(omega )=hbar omega {bigg (}n+{frac {1}{2}}{bigg )},quad n=0,1,dots ,} podobnie jak oscylator bozonowy). Częstotliwości mogą zaś przyjmować wartości dodatnie, continuum.

Stan pola fermionowego (np. przypisanego elektronowi, mające spin 1/2) opisuje się jako sumę wzbudzeń wielu oscylatorów fermionowych, które dla danej częstotliwości mogą przyjmować tylko dwa stany energii E0(ω)=−12ℏω{displaystyle E_{0}(omega )=-{frac {1}{2}}hbar omega } oraz E1(ω)=+12ℏω.{displaystyle E_{1}(omega )=+{frac {1}{2}}hbar omega .} Częstotliwości mogą zaś przyjmować wartości dodatnie, continuum.

Supersymetria |

Z połączenia hamiltonianu bozonowego i fermionowego tworzy się hamiltonian

H=12ℏω({a†,a}+[c†,c]).{displaystyle H={frac {1}{2}}hbar omega ({a^{dagger },a}+[c^{dagger },c]).}

Hamiltonian ten ma łącznie dodatkową symetrię, zwaną supersymetrią – miesza ona bozonowe stopnie swobody z fermionowymi. Symetria ta jest generowana przez operatory: Q=2ωa†c{displaystyle Q={sqrt {2omega }}a^{dagger }c} oraz Q†=2ωc†a,{displaystyle Q^{dagger }={sqrt {2omega }}c^{dagger }a,} które spełniają relację:

{Q,Q†}=2H.{displaystyle {Q,Q^{dagger }}=2H.}

Ta własność jest podstawą konstrukcji supersymetrycznej teorii pola.

Zobacz też |

• kwantowa teoria pola


• kwantowa teoria pola grawitacyjnego


• kwantowa teoria pola w zakrzywionej czasoprzestrzeni

Przypisy |

Bibliografia |

• R.L. Liboff: Wstęp do mechaniki kwantowej. Warszawa: PWN, 1987, s. 164–180.


• Claude Cohen-Tannoudji, Bernard Diu, Frank Laloë, Quantum Mechanics, Vol. I, 1991. Wiley, New-York, ​ISBN 0-471-16433-X​, s. 481–541.